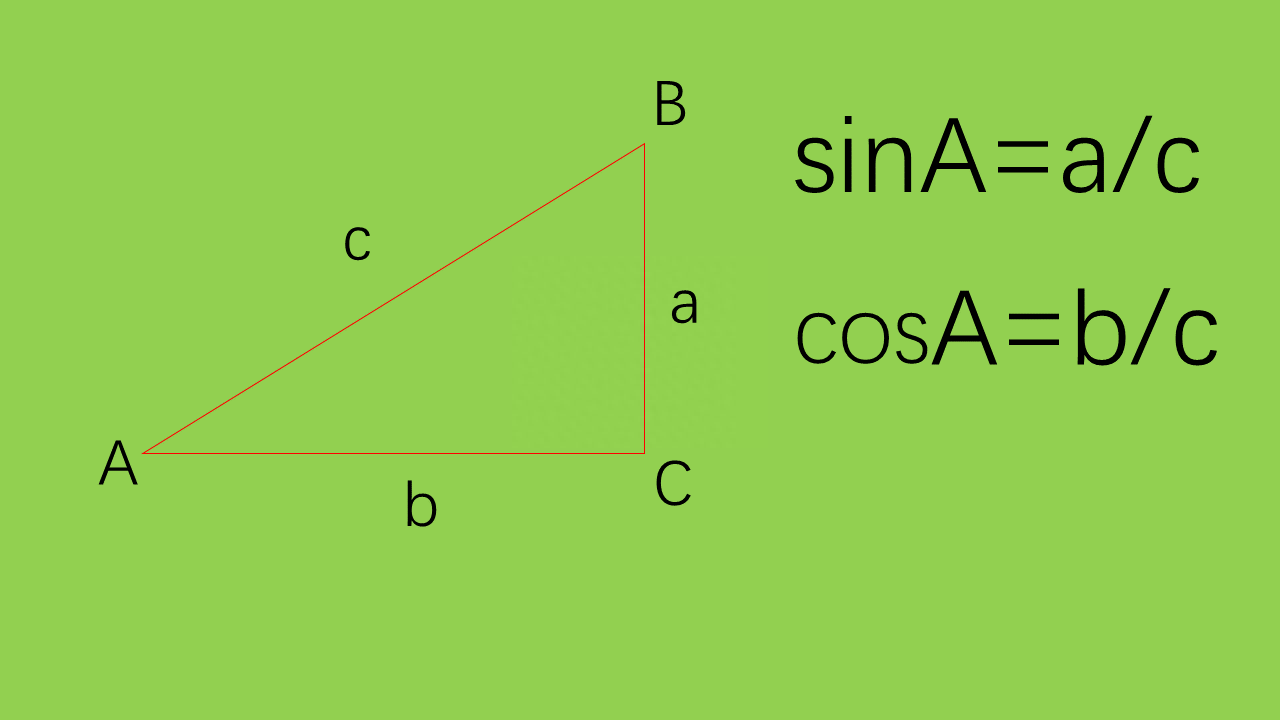任意角三角函数公式的定义 任意角三角函数怎么算
三角函数是最基本的初等函数之一,是以角度(数学上常以弧度制为基础)为自变量,角度对应任意角终边与单位圆交点坐标为应变量的函数。所以,我们要想理解三角函数,得从如下几个角度入手。

①特殊三角形中的三角函数我们在初中(我之前的文章也有提过)学习过三角函数的入门知识。如下图:即三角函数的定义,正限制是什么?余弦值又是什么?正切值又是什么?看图可以知道,正弦sin表示对边比斜边,而余弦cos表示邻边比斜边,正切tan表示对边邻边。这是最基本的概念,我们不需要知道为什么?因为数学家就是这样定义的,接下来我们要用这个概念了解任意角的三角函数。
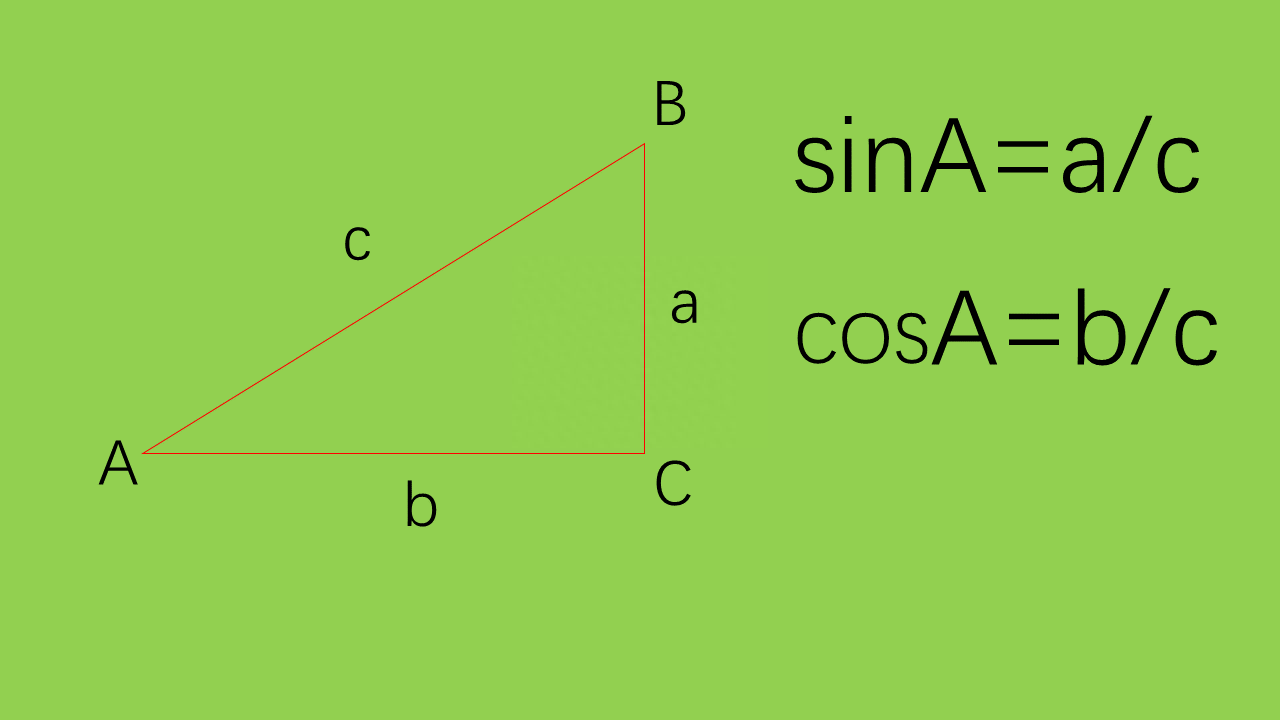
②任意三角函数,加坐标系,引入单位圆是基础了解了三角函数的基本定义是不够的,因为有的小伙伴发现无法求出sin167°的值。那么如何才可以求出呢?细心的朋友会发现,哎,不对啊,我们初中了解的知识不是完整的函数啊,只是其中的特殊例子,所以无法普遍应用很正常啊!那么今天我们就来正真了解一下三角函数。首先,把三角形放入坐标系中,如下图。接着引入单位圆(单位圆,斜边为1),我们会发现∠BOC的正弦值就等于B点的纵坐标,而它的余弦值就是他的横坐标。于是乎:B(cos∠BOC,sin∠BOC)
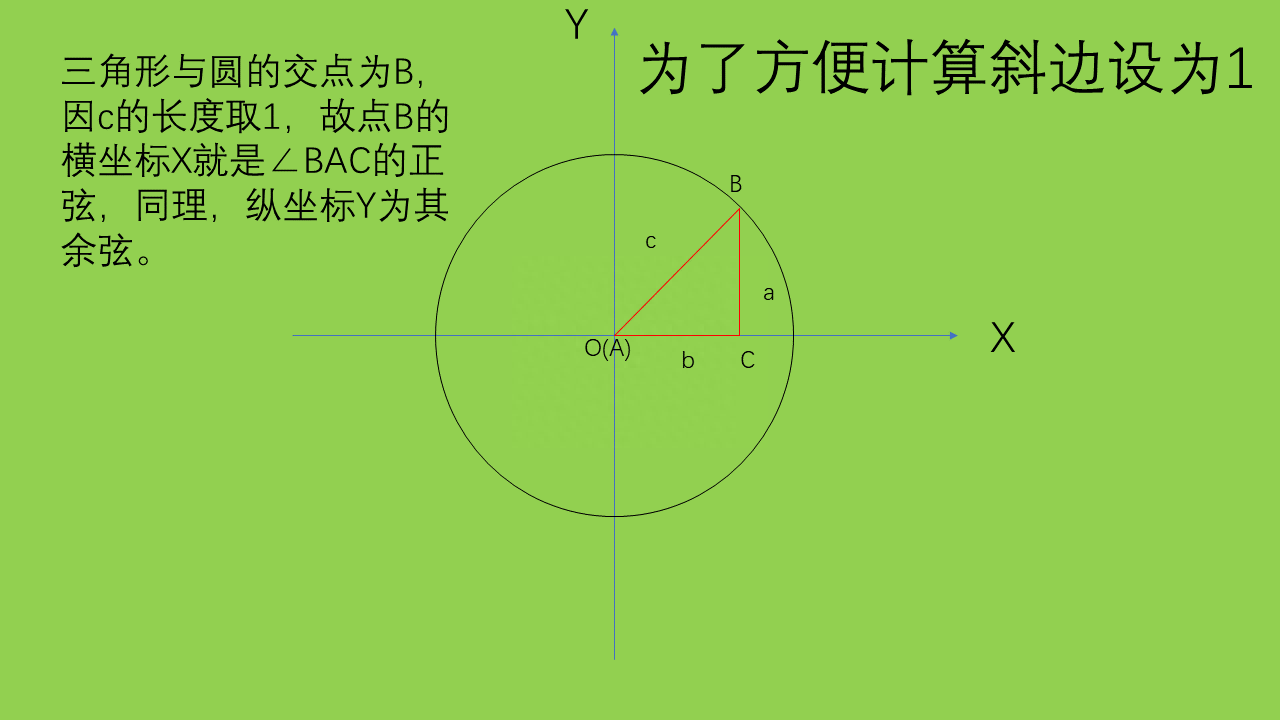
③任意角三角函数定义我们以OX为始边(X轴正半轴),O为轴心,开始逆时针旋转,OX与圆交点为C。我们会发现,当旋转角度为0°-90°时,就是我们初中接触过的三角函数,而大于90°小于180°的时候,就成了钝角的函数了。钝角的函数怎么求呢?我们通过上面结论,知道终边与圆的交点坐标就是旋转角度的正弦和余弦值。而在0°到180°,钝角的函数值都有锐角与其关于Y轴对称。而由对称知识可知,关于y对称,Y坐标不变,而X坐标互为相反数。即正弦不变,余弦互为相反数。即sinX=sin(180°-X),cosX=-cos(180°-X),得到这点,我们就可以把任意钝角转化为锐角,就可以求出其函数值了。于是有sin167°=sin13°
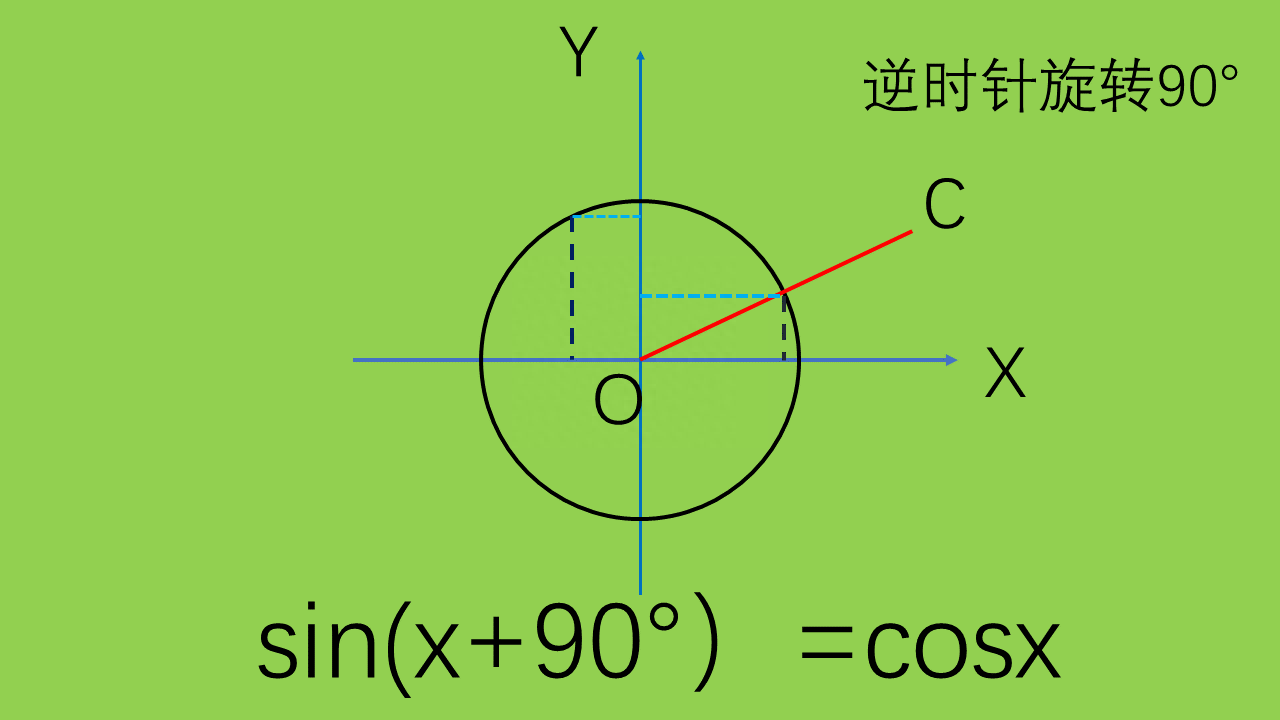
④两个特殊例子根据上面的思维,我们继续分析。当一个角分别加90°,180°时,结果又会如何呢?先加90°,我们会发现(看上图)这是它的终边交点坐标与之前角度相比有了变化。什么变化呢?仔细看一下会明白它的纵坐标是原图的横坐标,而横坐标是其纵坐标。于是可得公式:sinx=cos(90°+x)cosx=sin(90°+x)再来看180°的图形(下图),我们发现加180°之后,两个交点关于原点O对称。又初中对称知识可知,关于原点对称的两点,其横纵坐标互为相反数。于是,sinx=-sin(180°+x)cosx=-cos(180°+x)
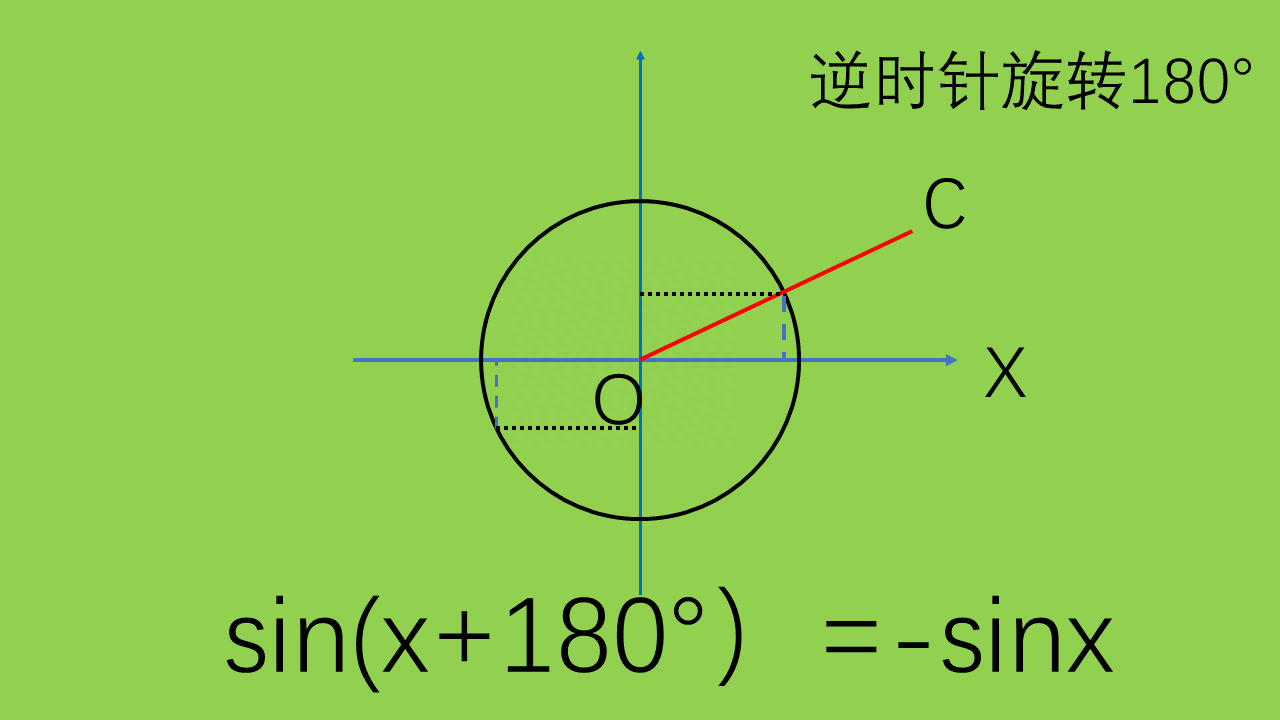
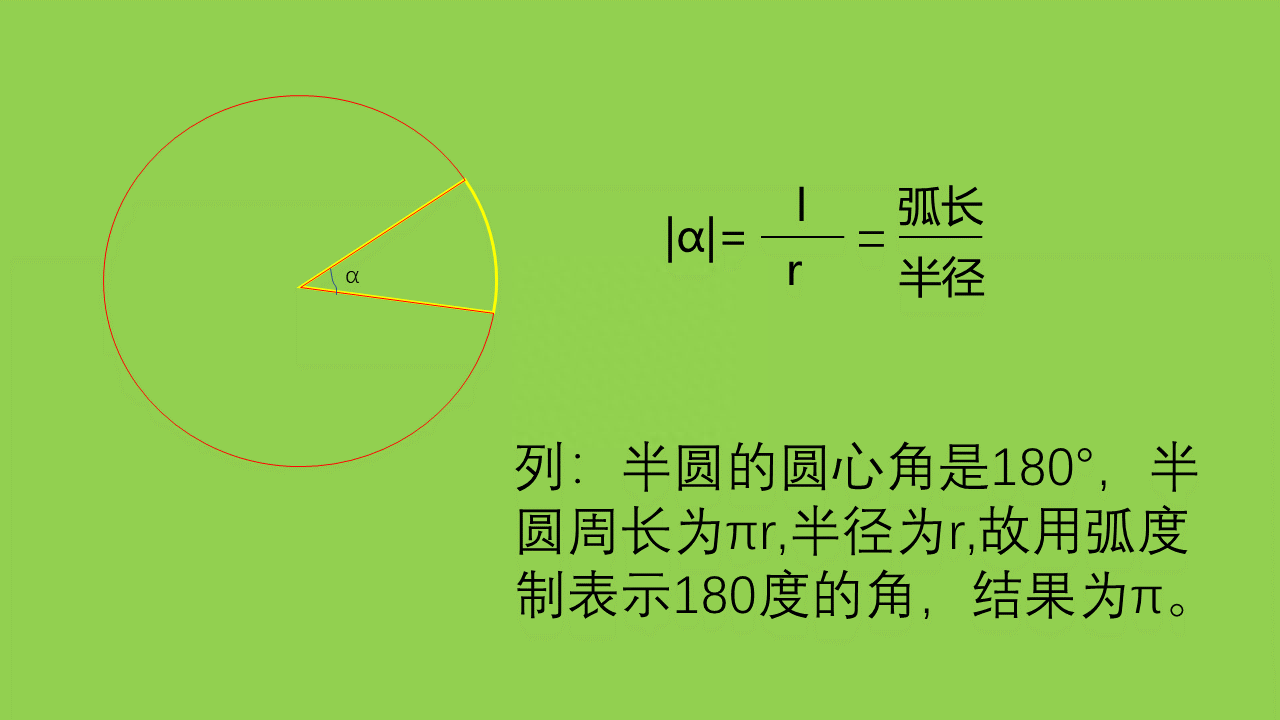
⑤弧度制三角函数是以角度为自变量的,为了方便运算,引入了弧度制。那么什么是弧度制呢?(看下图)弧长与半径的比就是弧的度数,于是180°的弧对应的弧度是π,90°=π/2,60°=π/3
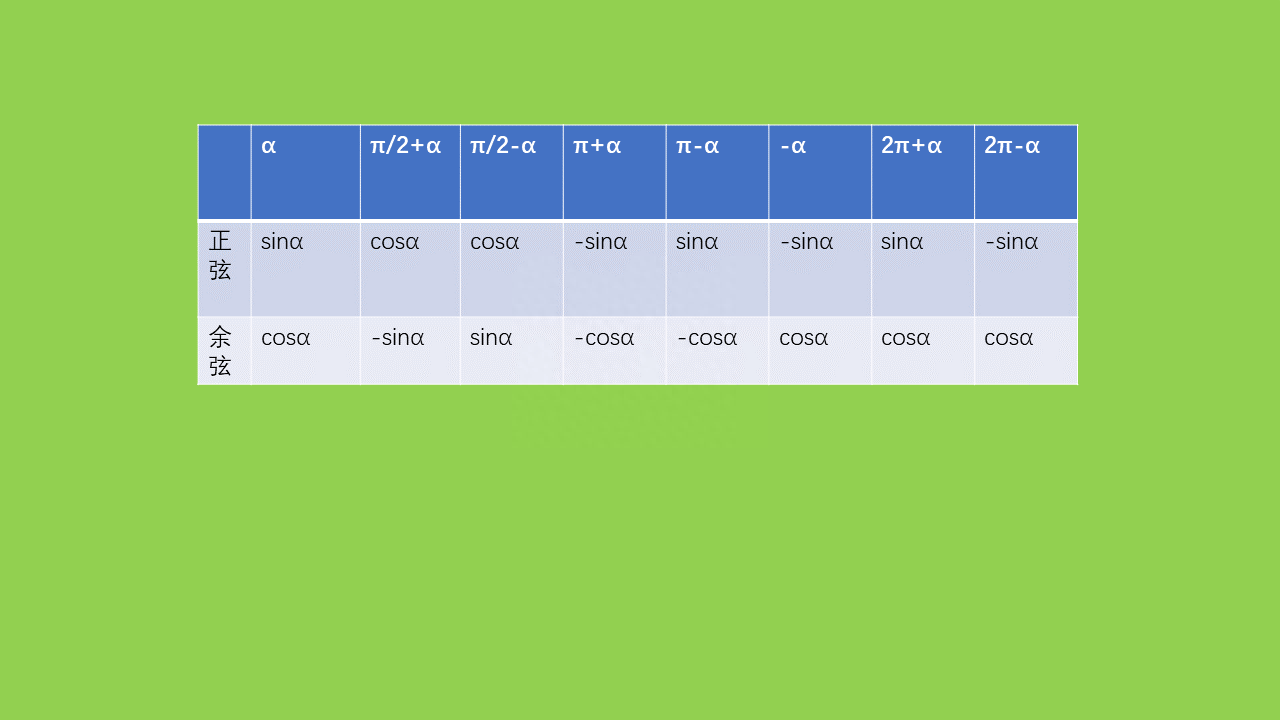
⑥几个基本的公式有了上面的基础,我觉得你看下表就应该可以看明白了吧!学三角函数的时候,老师都会给大家讲解公式的推导。有的朋友看一下不懂,就觉得把公式记住就可以了。于是,他就开始记下面的公式,然后经常出错。上面我给大家讲解了一下思路,希望大家按着这个思路把下面公式一个一个自己弄出来,这样我觉得你的三角函数这块就没多大问题了。
⑦思考题求出下面各函数值sin135°,cos135°,sin225°,cos225°欢迎大家评论区留言,我会第一时间回复大家。我是蓝色阿狸,记得关注我哦!有不明白的地方私聊我!
标签:

81
鸡胸肉简单怎么做好吃视频 鸡胸肉怎么做家常 对那些想要减肥的人而言,鸡胸肉是一个让他们既喜欢又讨厌的东西。怎么说的? 众所周知,在减肥的过程中,我们不能食用高热量的食...

189
小仙女们都沦陷了!奶萌皮卡丘OPPO R17 Pro主题掳获众心 以前提起双十一大家都想到“光棍”,现在积极的一面是,这已经全然是一场购物狂欢了!各商家和消费者们也都挖空心思大high一...

144
最新!涉及新机场建设,高明将获省专项资金 近日,广东省发展改革委关于下达2025年区域协调发展战略专项资金(重大项目前期工作经费)投资计划(第一批)的通知(以下简称“通...

59
韩国高分漫画《整容液》:迷恋整容的背后,是畸形腐化的心态 大家好,我是爱幻想的千事君。 关于韩国高分恐怖漫画《整容液》,相信大家都听说过。《整容液》漫画原著作者是韩...
59
FIFA ONLINE 4 当前版本大热球员推荐 合区后全国各地的玩家同服竞技,小伙伴们的排位之旅是不是更有挑战性了呢。之前许多粉丝留言说,想了解当前版本哪些球员比较强势,那么本期就...
113
腾讯柯凡喷NBA球星詹姆斯,看詹皇如何回应? 笑话也关注这个事了,据说柯凡被腾讯无限期停止,之前录音门就惹怒了广大詹密,但是你没做回应,慢慢的这事儿就过去了,现在又来作...

70
电影推荐,《心房客》,一个大写的孤独 心房客毕竟只是房客,但至少你已经走过了我的心。这部电影的每一帧都可以用作电脑桌面,每一张照片都是精心制作的。这个故事讲述了三个...

179
科拉超深钻井下所听到的“地狱之声”究竟是什么? 1970年,在俄罗斯的科拉半岛,一群研究人员开始了一个项目,他们想知道地下深处究竟存在着什么。 由于钻探很深,钻井经常发生...

62
刘珂矣《风筝误》解读 首先《风筝误》是刘珂矣演唱的一首 中国风 歌曲,于2015年6月24日发表,收录在专辑《半壶纱》中。然后这首歌曲的创作灵感源于一出清代昆曲剧目《风筝误》,...

59
九年的课本装进包包里?小小电视学习机让孩子爱上学习 快过年了,尤其是在外地打工带孩子的都准备和孩子一起回老家,带孩子出门总是大包小包,担心玩性大的孩子会影响学习,所...

135
杨玉环真容有多美?复原图酷似一女星,难怪唐玄宗会为她废弃后宫 【历史深处的美人:杨玉环,大唐盛世的绝代风华】 在历史的长河中,有些名字仿佛被岁月镌刻,熠熠生辉。杨玉...

156
素媛案罪犯放在我国,能被判多少年? 韩国电影《素媛》中犯罪嫌疑人的的原型赵斗顺即将出狱的消息不仅在韩国持续发酵,在中国也引发了极大的震动。 赵斗顺拥有着强烈的反社会...

180
女星杨幂到底多有钱,杨幂被爆身家达45亿?爸爸住十万一平的房子 提起杨幂,已经是家喻户晓了,4岁出道,在娱乐圈摸爬滚打了这么多年,如今已经一跃成为一线女星。 杨幂出生于...

58
日军不当少将也要争当大佐,日本“大佐”等于我军什么军衔? 近代日本军队改革中,许多理念与西方国家相似,但在军衔制度上,日本有一个独特的称谓,即“大佐”或“少佐”,这...

80
揭秘火化过程:人死后的奇妙之旅 导语:死亡是每个人都要面对的现实,而火化作为一种常见的葬礼方式,背后隐藏着许多不为人知的秘密。今天,就让我们一起揭开这层神秘的面纱,...

134
房价要崩盘了?一线城市的风云变幻背后藏着什么秘密? 最近关于一线城市房价要崩盘的传闻可真是搅动了不少人的心啊,搞得买房的、投资的都坐不住了。说白了,这楼市就像个不安...

82
法官怕什么,真的跟你没关系 网上有些文章或视频,说自己冒着被“迫害”的风险,介绍法官最怕什么。有说法官怕程序违法的,有说法官怕当事人打公开投诉电话的,还有说法官怕当...

143
电视剧《爱情悠悠药草香》民国时期医药世家白家的家族悲喜画卷。 在浩瀚的电视剧海洋中,有一部作品以其独特的背景和复杂的人物关系,吸引了无数观众的眼球,那就是《爱情悠悠...

125
安䘵山反唐,近20万胡汉将士为何义无反顾?对叛乱的了解如何? 【历史探索:安史之乱的惊世叛逆】 在中国历史的长河中,有一段惊世叛逆的篇章,那就是安史之乱。这场叛乱不仅仅...

96
重要通知!2018年肥东中考成绩可以查询啦(附查询链接)~还不赶紧戳进来 小伙伴们注意啦! 肥东中考成绩可以查询了 赶紧动动手查查自己分数吧~ 经过评卷、校验、统分合成及分析统...